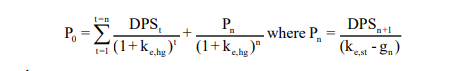- Study
- Slides
- Videos
8.1 Introduction
Since projections of dividends cannot be made through infinity, several versions of the dividend/cashflow discount model have been developed based upon different assumptions about future growth. Lets begin with the simplest – a model designed to value stock in a stable-growth firm that pays out what it can afford in dividends and then look at how the model can be adapted to value companies in high growth that may be paying little or no dividends.
8.2 The Gordon Growth Model
The Gordon growth model can be used to value a firm that is in ‘steady state’ with dividends growing at a rate that can be sustained forever. The Model The Gordon growth model relates the value of a stock to its expected dividends in the next time period, the cost of equity and the expected growth rate in dividends.
Value of Stock = DPS1/ ke-g where,
DPS1 = Expected Dividends one year from now (next period)
ke= Required rate of return for equity investors
g = Growth rate in dividends forever
What is a stable growth rate?
While the Gordon growth model is a simple and powerful approach to valuing equity, its use is limited to firms that are growing at a stable rate. There are two insights worth keeping in mind when estimating a ‘stable’ growth rate. First, since the growth rate in the firm’s dividends is expected to last forever, the firm’s other measures of performance (including earnings) can also be expected to grow at the same rate. To see why, consider the consequences in the long term of a firm whose earnings grow 6% a year forever, while its dividends grow at 8%. Over time, the dividends will exceed earnings.
On the other hand, if a firm’s earnings grow at a faster rate than dividends in the long term, the payout ratio, in the long term, will converge towards zero, which is also not a steady state. Thus, though the model’s requirement is for the expected growth rate in dividends, analysts should be able to substitute in the expected growth rate in earnings and get precisely the same result, if the firm is truly in steady state.
The second issue relates to what growth rate is reasonable as a ‘stable’ growth rate. This growth rate has to be less than or equal to the growth rate of the economy in which the firm operates. This does not, however, imply that analysts will always agree about what this rate should be even if they agree that a firm is a stable growth firm for three reasons:
-
Given the uncertainty associated with estimates of expected inflation and real growth in the economy, there can be differences in the benchmark growth rate used by different analysts, i.e., analysts with higher expectations of inflation in the long term may project a nominal growth rate in the economy that is higher.
-
The growth rate of a company may not be greater than that of the economy but it can be less. Firms can become smaller over time relative to the economy.
-
There is another instance in which an analyst may be stray from a strict limit imposed on the ‘stable growth rate’. If a firm is likely to maintain a few years of ‘above-stable’ growth rates, an approximate value for the firm can be obtained by adding a premium to the stable growth rate, to reflect the above-average growth in the initial years. Even in this case, the flexibility that the analyst has is limited.
8.3 Two-Stage Dividend Discount Model
The two-stage growth model allows for two stages of growth – an initial phase where the growth rate is not a stable growth rate and a subsequent steady state where the growth rate is stable and is expected to remain so for the long term. While, in most cases, the growth rate during the initial phase is higher than the stable growth rate, the model can be adapted to value companies that are expected to post low or even negative growth rates for a few years and then revert back to stable growth.
The Model The model is based upon two stages of growth, an extraordinary growth phase that lasts n years and a stable growth phase that lasts forever afterwards. Extraordinary growth rate: g% each year for n years and then stable growth: gn forever
Value of the Stock = PV of Dividends during extraordinary phase + PV of terminal price
where,
DPSt = Expected dividends per share in year t
ke = Cost of Equity (hg: High Growth period; st: Stable growth period)
Pn = Price (terminal value) at the end of year n
g = Extraordinary growth rate for the first n years
gn = Steady state growth rate forever after year n
This model is best suited for firms which are in high growth and expect to maintain that growth rate for a specific time period, after which the sources of the high growth are expected to disappear. One scenario, for instance, where this may apply is when a company has patent rights to a very profitable product for the next few years and is expected to enjoy super-normal growth during this period. Once the patent expires, it is expected to settle back into stable growth. Another scenario where it may be reasonable to make this assumption about growth is when a firm is in an industry which is enjoying super-normal growth because there are significant barriers to entry (either legal or as a consequence of infra-structure requirements), which can be expected to keep new entrants out for several years.
The assumption that the growth rate drops precipitously from its level in the initial phase to a stable rate also implies that this model is more appropriate for firms with modest growth rates in the initial phase. For instance, it is more reasonable to assume that a firm growing at 12% in the high growth period will see its growth rate drops to 6% afterwards than it is for a firm growing at 40% in the high growth period. Finally, the model works best for firms that maintain a policy of paying out most of residual cash flows – i.e, cash flows left over after debt payments and reinvestment needs have been met – as dividends.
8.4 The Three Stage Model
The three-stage dividend discount allows for an initial period of high growth, a transitional period where growth declines and a final stable growth phase. It is the most general of the models because it does not impose any restrictions on the payout ratio.
The value of the stock is then the present value of expected dividends during the high growth and the transitional periods and of the terminal price at the start of the final stable growth phase.
This model’s flexibility makes it a useful model for any firm, which in addition to changing growth over time is expected to change on other dimensions as well – in particular, payout policies and risk. It is best suited for firms which are growing at an extraordinary rate now and are expected to maintain this rate for an initial period, after which the differential advantage of the firm is expected to deplete leading to gradual declines in the growth rate to a stable growth rate. Practically speaking, this may be the more appropriate model to use for a firm whose earnings are growing at very high rates, are expected to continue growing at those rates for an initial period, but are expected to start declining gradually towards a stable rate as the firm become larger and loses its competitive advantages.