Learn About Measuring Risk & Return of Mutual Fund

5.1 Risk Return Relationship

The most fundamental tenet of finance literature is that there is a trade-off between risk and return. The risk-return relationship requires that the return on a security should be commensurate with its riskiness. If the capital markets are operationally efficient, then all investment assets should provide a rate or return that is consistent with the risks associated with them. The risk and return are directly variable, i.e., an investment with higher risk should produce higher return.

The risk/return trade-off could easily be called the “ability-to-sleep-at-night test.” While some people can handle the equivalent of financial skydiving without batting an eye, others are terrified to climb the financial ladder without a secure harness. Deciding what amount of risk you can take while remaining comfortable with your investments is very important.

In the investing world, the dictionary definition of risk is the possibility that an investment’s actual return will be different than expected. Technically, this is measured in statistics by standard deviation. Risk means you have the possibility of losing some, or even all, of your original investment.

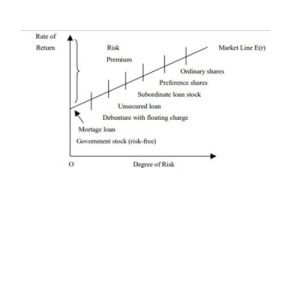
Low levels of uncertainty (low risk) are associated with low potential returns. High levels of uncertainty (high risk) are associated with high potential returns. The risk/ return trade-off is the balance between the desire for the lowest possible risk and the highest possible return. This is demonstrated graphically in the chart below. A higher standard deviation means a higher risk and higher possible return. The figure below represents the relationship between risk and return.

The slope of the Market Line indicates the return per unit of risk required by all investors. Highly risk-averse investors would have a steeper line, and vice versa. Yields on apparently similar stocks may differ. Differences in price, and therefore yield, reflect the market’s assessment of the issuing company’s standing and of the risk elements in the particular stocks. A high yield in relation to the market in general shows an above average risk element

Risk & return relationship of various securities

Given the composite market line prevailing at a point of time, investors would select investments that are consistent with their risk preferences. Some will consider low-risk investments, while others prefer high-risk investments.

A common misconception is that higher risk equals greater return. The risk/return tradeoff tells us that the higher risk gives us the possibility of higher returns. But there are no guarantees. Just as risk means higher potential returns, it also means higher potential losses.

On the lower end of the scale, the risk-free rate of return is represented by the return on Treasury Bills of government securities, because their chance of default is next to nil. If the risk-free rate is currently 8 to 10 %, this means, with virtually no risk, we can earn 8 to 10 % per year on our money. The common question arises: who wants to earn 6% when index funds average 12% per year over the long run? The answer to this is that even the entire market (represented by the index fund) carries risk. The return on index funds is not 12% every year, but rather -5% one year, 25% the next year, and so on. An investor still faces substantially greater risk and volatility to receive an overall return that is higher than a predictable government security. This additional return is the risk premium, which in this case is 8% (12% – 8%). Determining what risk level is most appropriate for you isn’t an easy question to answer. Risk tolerance differs from person to person. The decision should depend on your goals, income and personal situation, among other factors.

5.2 Portfolio and Security Returns

A portfolio is a collection of securities. Since it is rarely desirable to invest the entire funds of an individual or an institution in a single security, it is essential that every security be viewed in a portfolio context. Thus, it seems logical that the expected return of a portfolio should depend on the expected return of each of the security contained in the portfolio. It also seems logical that the amounts invested in each security should be important. Indeed, this is the case.

The example of a portfolio with three securities shown below that illustrates this point.

Security and Portfolio Values

Security and Portfolio Value-Relative

Security and Portfolio Holding-period Returns

Since the portfolio’s expected return is a weighted average of the expected returns of its securities, the contribution of each security to the portfolio’s expected returns depends on its expected returns and its proportionate share of the initial portfolio’s market value. Nothing else is relevant. It follows that an investor who simply wants the greatest possible expected return should hold one security. This should be the one that is considered to have the greatest expected return. Very few investors do this, and very few investment advisers would counsel such an extreme policy. Instead, investors should diversify, meaning that their portfolio should include more than one security. This is because diversification can reduce risk.

5.3 Risk and Return Calculation

Lets take an example of a single security also and understand its return calculation. The table below shows the average market price and dividend per share of SAIL Limited for the past 6 years:

So, avg return for SAIL Limited would be:

Average Return= (19.09+12.42+13.41-4.07+20.57)/5= 12.28%

Lets calculate the standard deviation for SAIL Limited considering certain probabilities for occurrence of each of these returns

Average Return= 12.28%

Standard Deviation= √50.447 = 7.10%

5.4 Return Calculation of Portfolio ( Two Assets)

The expected return from a portfolio of two or more securities is equal to the weighted average of the expected returns from the individual securities.

Where,

ε(Rp)= Expected return from a portfolio of two securities

Wa= Proportion of funds invested in Security A

Wb= Proportion of funds invested in Security B

Ra = Expected return of Security A

Rb= Expected return of Security B

Wa+Wb=1

Lets take an example: Ms. Ridhi’s portfolio consist of 6 securities and individual weight and return of each security is given below.

The weighted avg return would be: (0.10*18)+(0.25*12)+(0.08*22)+(0.30*15)+(0.12*6)+(0.15*8)

= 12.98%

5.5 Return Calculation of Portfolio ( Two Assets)

The risk of a security is measured in terms of variance or standard deviation of its returns. The portfolio risk is not simply a measure of its weighted average risk. The securities that a portfolio contains are associated with each other. The portfolio risk also considers the co-variance between the returns of the investment. Covariance of two securities is a measure of their co-movement; it expresses the degree to which the securities vary together.

The standard deviation of a two-share portfolio is calculated by applying formula given below:

The covariance of Security A and Security ( ) can be presented as follows:

CovAB = qA qB PAB

The diversification of unsystematic risk, using a two-security portfolio, depends upon the correlation that exists between the returns of those two securities. The quantification of correlation is done through calculation of correlation coefficient of two securities (rAB). The value of correlation ranges between – 1 to 1; it can be interpreted as follows:

If

PAB = 1, No unsystematic risk can be diversified.

PAB = – 1, All unsystematic risks can be diversified.

PAB = 0, No correlation exists between the returns of Security A and Security B.

The returns of Security of Wipro and Security of Infosys for the past five years are given below:

Mean Return & Standard Deviation of Wipro

Mean Return= 45/5= 9%

Standard Deviation= √110= 10.49%

Mean Return & Standard Deviation of Infosys

Mean Return= 40/5= 8%

Standard Deviation= √266= 16.31%

Analysis – Wipro has a higher historic level of return and lower risk as compared to Infosys

Co-variance of Returns of Infosys & Wipro

P_AB= COV_AB/ q_A q_B= 84/(10.49*16.31)= 0.491

COV_AB= q_A q_B P_AB= 10.49*16.31*0.491= 84

Return of portfolio (Rp ) = (0.80 * 9) + (0.20* 8) = 7.2 + 1.6 = 8.8%

Risk of portfolio (q_p ) = (0.80² *10.49² ) + (0.20² *16.31² ) + (2 *0.80 * 0.20 * 10.49 * 16.31 * 0.491)

= (0.64 *110.04) + (0.04 * 266.02) + 26.88

= 70.43 + 10.64 + 26.88 = 107.95

(q_p ) = √107.95 = 10.39%