Learn About Capital Asset Pricing Model

9.1 Introduction

William F. Sharpe and John Linter developed the Capital Asset Pricing Model (CAPM). The model is based on the portfolio theory developed by Harry Markowitz. The model emphasises the risk factor in portfolio theory is a combination of two risks, systematic risk and unsystematic risk. The model suggests that a security’s return is directly related to its systematic risk, which cannot be neutralised through diversification. The combination of both types of risks stated above provides the total risk. The total variance of returns is equal to market related variance plus company’s specific variance. CAPM explains the behaviour of security prices and provides a mechanism whereby investors could assess the impact of a proposed security investment on the overall portfolio risk and return.

CAPM suggests that the prices of securities are determined in such a way that the risk premium or excess returns are proportional to systematic risk, which is indicated by the beta coefficient. The model is used for analysing the risk-return implications of holding securities. CAPM refers to the manner in which securities are valued in line with their anticipated risks and returns. A risk-averse investor prefers to invest in risk-free securities. For a small investor having few securities in his portfolio, the risk is greater. To reduce the unsystematic risk, he must build up well-diversified securities in his portfolio.

The asset return depends on the amount for the asset today. The price paid must ensure that the market portfolio’s risk/return characteristics improve when the asset is added to it. The CAPM is a model, which derives the theoretical required return (i.e. discount rate) for an asset in a market, given the risk-free rate available to investors and the risk of the market as a whole.

The CAPM is usually expressed:

E(Ri ) = Rf + β (E(Rm)-Rf )

β(Beta), is the measure of asset sensitivity to a movement in the overall market; Beta is usually found via regression on historical data. Betas exceeding one signify more than average “riskiness”; betas below one indicate lower than average.

E(Rm)-(Rf ) is the market premium, the historically observed excess return of the market over the risk-free rate.

Once the expected return, E(Ri ), is calculated using CAPM, the future cash flows of the asset can be discounted to their present value using this rate to establish the correct price for the asset. (Here again, the theory accepts in its assumptions that a parameter based on past data can be combined with a future expectation.)

A more risky stock will have a higher beta and will be discounted at a higher rate; less sensitive stocks will have lower betas and be discounted at a lower rate. In theory, an asset is correctly priced when its observed price is the same as its value calculated using the CAPM derived discount rate. If the observed price is higher than the valuation, then the asset is overvalued; it is undervalued for a too low price.

9.2.Assumptions of CAPM

Because the CAPM is a theory, we must assume for argument that:

1. All assets in the world are traded.
2. All assets are infinitely divisible.
3. All investors in the world collectively hold all assets.
4. For every borrower, there is a lender.
5. There is a riskless security in the world.
6. All investors borrow and lend at the riskless rate.
7. Everyone agrees on the inputs to the Mean-STD picture.
8. Preferences are well described by simple utility functions.
9. Security distributions are normal, or at least well described by two parameters.
10. There are only two periods of time in our world.

This is a long list of requirements, and together they describe the capitalist’s ideal world. Everything may be bought and sold in perfectly liquid fractional amounts even human capital! There is a perfect, safe haven for risk-averse investors i.e. the riskless asset. This means that everyone is an equally good credit risk! No one has any informational advantage in the CAPM world.

9.3.Analysis of CAPM

To analyze the CAPM, let us review the understanding of systematic and unsystematic risk explained in the earlier chapters.

A. Systematic Risk:

This is the part of total risk comprising of systematic and unsystematic risk. Systematic risk cannot be eliminated. It is part of market risk, government policies, economic situations like inflation or recession and other policies of tax and credit. Since this risk cannot be eliminated securities may be diversified to minimize it. Systematic risk is also called market risk and it is measured by Beta. According to William Sharpe the Beta coefficient is the relative measure of sensitivity of an asset change, to the change in the return of the market portfolio. Beta is calculated as the securities covariance with the market portfolio divided by the variance of the market portfolio. When Beta factor increases the expected return also increases.

β= Cov (S,M)/ q²_M= q_s*q_M*R_SM/q²_M= q_s/q_M* R_SM

Where,

COV (S,M) = Covariance between the return of security S, and the return on the market Portfolio,

M = Standard deviation of the security, S

q_M= Standard deviation of the market portfolio, M

q²_M=Variance of the return of market portfolio, M

R_SM= Correlation between the return of the security and the market portfolio.

B. Unsystematic Risk:

This risk can be eliminated by diversification. It is based on individual risk specific to a particular company or industry. Some examples are labour strike, change in consumer preferences and company policies in financial or marketing matters. This risk can be diversified and eliminated unlike the systematic risk.

C. CAPM and Risk:

A portfolio which does not have any unsystematic risk will be called an efficient portfolio. Therefore, in a portfolio constructed through CAPM only systematic risk is relevant. Total risk can be measured by standard deviation but Beta measures systematic risk. In CAPM Beta risk or systematic risk is considered for pricing of securities

D. Market Portfolio:

The portfolio comprising of different securities in the market is called the market portfolio. The return of the market portfolio is the difference between the expected market return and risk-free interest multiplied by Beta factor

9.4. Security Market Line

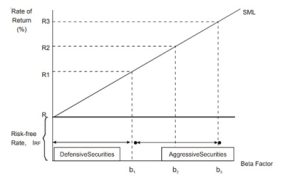
The security market line gives an explanation about the relationship between the required rate of return on a security/portfolio and its Beta factor. It is the graphical version of the CAPM.

In Figure below the required rate of return is depicted as R1, R2 and R3 with the respective Beta factors β 1, β 2 and β 3. When the Beta factor is zero it is represented by the intercept OR or the risk-free rate of return. When Beta factor increases the premium on return also increases. Therefore, low Beta provides low risk and also low return. The risk and return of securities is determined by beta. All portfolios lie along a straight-line on which the beta is measured. The point which is a riskless asset of beta O is the first point.

Beta 1 is the second point on the market line of the portfolio. This draws out the return which an investor expects on his assets on this portfolio whether they are efficient portfolio or inefficient portfolio.

The security market line as shown Figure below, shows that the security market line depends on the risk-free rate of return and the change in the required rate of return due to changes in the Beta factor. Therefore, the security market line depends on the required rate of return and the change in Beta factor.

Figure depicts that upto β 1 the securities are called defensive securities and beyond β 1 they are called aggressive securities. The point where β = 1 has an expected market return. The securities that have β < 1 do not have risk and because of this they are defensive. β > 1 show that the securities are riskier than the market. That is why they are called aggressive securities. Thus, SML is associated with positive slope which shows that the expected return increases with Beta.

9.5 Limitations of CAPM Model

The CAPM theory provides and understanding of measuring the return of a security depending on its systematic risk. It has certain limitations:

1. The assumption in the CAPM approach that investors have no transaction cost in purchase and sale of securities is not realistic.
2. It measures only market risk and gives importance to Beta or systematic risk and examines the historical returns to the market portfolio. Therefore Beta is difficult to measure for future returns until it is updated. This is problematic to calculate. Many calculations are involved and training is required for measurement.
3. The CAPM theory assumes that the investor can borrow or lend at the risk-free rate at any time and for any amount, this is not realistic.
4. The CAPM assumes that every investor has equal information and is available to all the investors. This is possible when the market is in the strong form of efficiency. Therefore information is uneven and cannot exist at the same level for every investor.