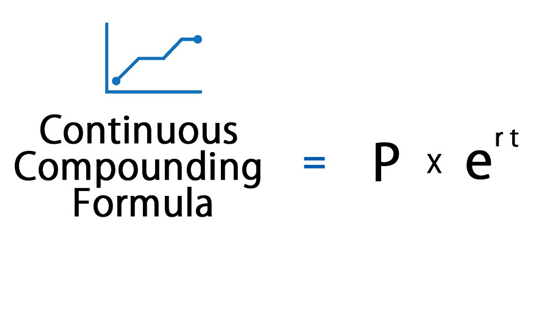निरंतर कंपाउंडिंग क्या है?

निरंतर कंपाउंडिंग क्या है?

निरंतर कंपाउंडिंग कंपाउंड ब्याज़ की गणना की सीमा है जहां ब्याज़ को अकाउंट के बैलेंस में अनंत बार दोबारा इन्वेस्ट किया जाता है. यह ब्याज़ घटक और पूरे इन्वेस्टमेंट के पोर्टफोलियो की वैल्यू को बढ़ाता है. हालांकि यह वास्तविक दुनिया में व्यावहारिक नहीं हो सकता है, लेकिन यह फाइनेंशियल दुनिया में आवश्यक है. 

इसके अलावा, यह एक स्पोरेडिक कंपाउंडिंग मामला है क्योंकि अधिकांश प्राप्त ब्याज़ मासिक, त्रैमासिक, अर्ध-वार्षिक या वार्षिक रूप से कंपाउंड किया जाता है. आसान शब्दों में, निरंतर कंपाउंडिंग यह मानती है कि ब्याज़ को कंपाउंड किया जाता है और स्रोत अकाउंट में वापस जोड़ दिया जाता है. इसका मतलब यह है कि अकाउंट नियमित रूप से ब्याज़ अर्जित करता है, बैलेंस में उसी ब्याज़ को दोबारा इन्वेस्ट करता है, और इस पर दोबारा ब्याज़ अर्जित करता है.

निरंतर कंपाउंडिंग का महत्व

यहां कुछ कारण दिए गए हैं कि निरंतर कंपाउंडिंग आवश्यक क्यों है:

• यह दिखाता है कि जब ब्याज़ प्राप्त होता है तो कितना बैलेंस अर्जित किया जा सकता है.
• यह निवेशकों को यह गणना करने में मदद करता है कि वे अपने निवेश से कितनी उम्मीद कर सकते हैं, जिससे लगातार कंपाउंडिंग ब्याज अर्जित होता है.
• यह इन्वेस्टर को इस बारे में सही निर्णय लेने में मदद करता है कि इस अर्जित ब्याज को अधिक लाभ प्राप्त करने के लिए कहां दोबारा इन्वेस्ट करना है.
• यह साधारण ब्याज से तेज़ राशि भी बढ़ाता है, क्योंकि बाद में केवल मूल राशि पर ही गणना की जाती है.
• कंपाउंडिंग के माध्यम से, पैसे को बढ़ी हुई दर पर गुणा किया जाता है. अधिक कंपाउंडिंग अवधि, अधिक कंपाउंड ब्याज होगा.
• यह विशेष रूप से लंबे समय में इन्वेस्टमेंट रिटर्न को भी बढ़ा सकता है.

निरंतर कम्पाउंडिंग फॉर्मूला

अब जब आप निरंतर कंपाउंडिंग का अर्थ समझ चुके हैं, तो इसके फॉर्मूले को देखने का समय है. नीचे कंपाउंडेड निरंतर फॉर्मूला दिया गया है:

A= पर्ट

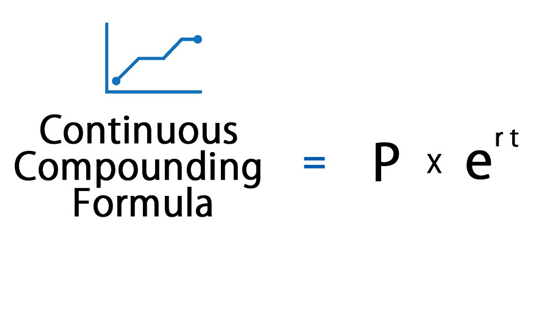
कंपाउंडिंग फॉर्मूला की गणना

यहां इस सेक्शन में, आइए लगातार कंपाउंड ब्याज़ फॉर्मूला के विभिन्न तत्वों को समझते हैं:
A= पर्ट 

उपरोक्त में,

A = अंतिम राशि
P = प्रारंभिक राशि
R = ब्याज दर
t = समय 
E = गणितीय स्थिर, जहां E = 2.7183

इस गणना में, समय बदलता है कि इसे कम्पाउंड करने की योजना कैसे बनाया जाता है. अगर यह तिमाही है, तो समय 1/4th होगा. 

अगर यह द्वि-वार्षिक रूप से किया जाता है, तो समय 1/2th होगा; अगर यह वार्षिक रूप से किया जाता है, तो यह 1/365 होगा. 

यह गणना घंटे, मिनट या दैनिक आधार पर भी हो सकती है. और व्यावहारिक शब्दों में, जो कोई मूल्य नहीं बनाता क्योंकि अंतर केवल दशमलव बिंदुओं में होगा. 

निरंतर कंपाउंडिंग फॉर्मूला कैसे प्राप्त करें?

कंपाउंड ब्याज़ फॉर्मूला से लगातार कंपाउंडिंग फॉर्मूला प्राप्त किया जाता है. कंपाउंड ब्याज़ फॉर्मूला नीचे दिए गए हैं:
A = P (1 + r/n)nt

उपरोक्त में,

A = अंतिम राशि या भविष्य मूल्य भी कहा जा सकता है
P = प्रारंभिक राशि
N = यह बार P की संख्या है या प्रारंभिक राशि कम्पाउंडिंग है
t = समय
R = ब्याज़ दर

निरंतर कंपाउंड ब्याज़ के मामले में, n →. तो, उपरोक्त सूत्र में सीमा है 
A = LIMNND → P (1 + r/n)nt = पर्ट

बाद में, अंतिम चरण में, लिमिट फॉर्मूला में से एक का इस्तेमाल किया जाता है: limn→ (1 + r/n)n = er.

और वहाँ से, निरंतर कंपाउंडिंग फॉर्मूला प्राप्त किया जाता है, जो है  

A= पर्ट

निरंतर कंपाउंडिंग का उपयोग कैसे करें के उदाहरण
आइए एक उदाहरण की मदद से फॉर्मूला का उपयोग करके समझते हैं. 

उदाहरण के लिए: बैंक में जमा की गई प्रारंभिक राशि ब्याज़ दर पर रु. 2340 है: वार्षिक आधार पर 3.1%. तीन (3) वर्षों के बाद बैलेंस क्या होगा?

इसलिए, यह फॉर्मूला कहता है, A= पर्ट

उपरोक्त उदाहरण से, P = 2340, 
आर = 3.1, जो 3.1/100 = 0.031 होगा
t = 3 (क्योंकि हमें 3 वर्षों के लिए गणना करनी होगी)
e = नेपियर का नंबर, जो लगभग 2.7183 है

आइए गणना करते हैं:
A = 2340 e0.031(3) ≈ 2568.06

इसलिए, तीन वर्षों के बाद, प्राप्त राशि रु. 2568.05 होगी

सरल ब्याज बनाम कंपाउंड ब्याज
इन दोनों की गणना कैसे की जाती है इसमें अंतर है. 

साधारण ब्याज़ एक निश्चित अवधि के बाद प्रारंभिक मूलधन राशि पर प्राप्त ब्याज़ है. ऐसे मामलों में, ब्याज़ शुरुआती राशि में नहीं जोड़ा जाता है. ब्याज़ का भुगतान एक निश्चित समय पर शुरुआती राशि पर किया जाता है. 

दूसरी ओर, कंपाउंड ब्याज़ में, प्रारंभिक मूलधन राशि अर्जित ब्याज़ को समायोजित करने के लिए बदलती है. इसलिए, प्रत्येक वर्ष, आपको प्राप्त होने वाली राशि का पिछले वर्ष का ब्याज़ शुरुआती मूल राशि में जोड़ा जाएगा.

निष्कर्ष

यह फॉर्मूला प्रारंभिक मूल राशि पर अर्जित ब्याज़ की जांच करता है. इस मामले में, कंपाउंडिंग समय को अक्सर अनंत माना जाता है. हालांकि निरंतर कंपाउंडिंग में आसान ब्याज़ से अधिक राशि की अंतिम वैल्यू दिखाई देती है, लेकिन यह वास्तविक विश्व मामलों में अप्लाई करना चुनौतीपूर्ण है. इसलिए, वास्तविक जीवन में इस्तेमाल करना बहुत व्यावहारिक नहीं हो सकता है क्योंकि इसमें फाइनेंशियल दुनिया में महत्वपूर्ण महत्व है. 

इसके बजाय, यह निवेशक के अंत से मूल्य धारण करता है. इन्वेस्टर 'X' इन्वेस्टमेंट पर प्राप्त होने वाली राशि को चेक कर सकते हैं और भविष्य के इन्वेस्टमेंट प्लान का निर्णय ले सकते हैं.