Akash Bhansali Portfolio 2026: An Insight into Top Stocks
Modern Portfolio Theory
Last Updated: 7th September 2023 - 05:01 pm
Modern Portfolio Theory is a mathematical framework using which investors can create a portfolio that allows them to maximise the return on their investments at any level of risk. As such, for every level of risk, the expected return from a set of investments will be different as per the Modern Portfolio Theory.
Who created Modern Portfolio Theory?
The father of the Modern Portfolio Theory is the American economist Harry Markowitz. Markowitz outlined the theory in a paper called ‘Portfolio Selection’, published in March 1952 in The Journal of Finance.
Born in August 1927, Markowitz studied at the University of Chicago, where he was chosen as one of the student members of the Cowles Commission for Research in Economics.
In 1989, thirty-seven years after Markowitz’s paper was published in The Journal of Finance, he was awarded the Von Neumann Prize in Operations Research Theory by the Operations Research Society of America and The Institute of Management Sciences. A year later, in 1990, he won the Nobel Prize in Economics jointly with fellow economists Merton Miller and William Sharpe.
Markowitz is currently the adjunct professor of finance at University of California San Diego’s Rady School of Management.
What is Modern Portfolio Theory?
For his dissertation, Markowitz landed upon the idea of applying mathematical models to the stock market.
“The basic concepts of portfolio theory came to me one afternoon in the library while reading John Burr Williams’s Theory of Investment Value. Williams proposed that the value of a stock should equal the present value of its future dividends. Since future dividends are uncertain, I interpreted Williams’s proposal to be to value a stock by its expected future dividends. But if the investor were only interested in expected values of securities, he or she would only be interested in the expected value of the portfolio; and to maximize the expected value of a portfolio one need invest only in a single security,” Markowitz has said.
“This, I knew, was not the way investors did or should act. Investors diversify because they are concerned with risk as well as return,” he went on to add.
As described above by Markowitz, an investor cares about both risk and return. What the Modern Portfolio Theory does is it allows investors to maximise returns for any acceptable level of risk of the entire portfolio of assets.
Return on a portfolio
An underlying assumption of the Modern Portfolio Theory is that investors are risk averse and would therefore, when given a choice between two portfolios that are expected to provide the same rate of return on investment, pick the less risky option.
As such, any higher risk will require compensation in the form of a higher rate of return; or, the pursuit of higher returns will require an investor to take on greater risk.
The expected return of a portfolio can be calculated by weighing each asset’s return with the size of investment made in that asset. For example, consider a portfolio consisting of investments in three assets: A, B, and C, offering an expected rate of return of 5%, 10%, and 20%, respectively. Assuming the total investment is allocated equally between these three assets, the portfolio's expected return would be:
(5% x 33.3%) + (10% x 33.3%) + (20% x 33.3%), or 11.7%.
Risk of a portfolio
The risk, or variance, attached to a portfolio can be measured by examining the riskiness of each asset and correlations of each asset pair. For our portfolio above comprising assets A, B, and C, the risk can be calculated by the sum of multiples of each asset’s weight in the portfolio and its variance along with the covariance between each of the assets.
As a general rule, assets in a portfolio should be selected if they have low or negative correlation with each other.
The square root of the portfolio variance is also called its standard deviation and paints a picture of volatility. A larger standard deviation means greater asset movement over time. And assets with a wider range of movement are riskier.
If assets in a portfolio are perfectly positive correlated with each other, then it increases the standard deviation, and therefore risk, of the portfolio.
Risk-free rate
A risk-free rate of return is that rate which guarantees a return to an investor with zero risk. While hypothetical examples can be constructed for risk-free assets, there are no such assets in reality as every asset carries some risk.
The least risky of all assets are debt instruments issued by governments. However, even government bonds are not completely risk free, with there being instances of governments choosing not to make repayments on their borrowing in the event of an economic crisis.
Portfolio frontier
Once a range of risks an investor is willing to accept is known, the Modern Portfolio Theory formula can be used to construct a variety of portfolios. On a graph with standard deviation on the X-axis and expected return on the Y-axis, the portfolio frontier is in the shape of a deformed C.
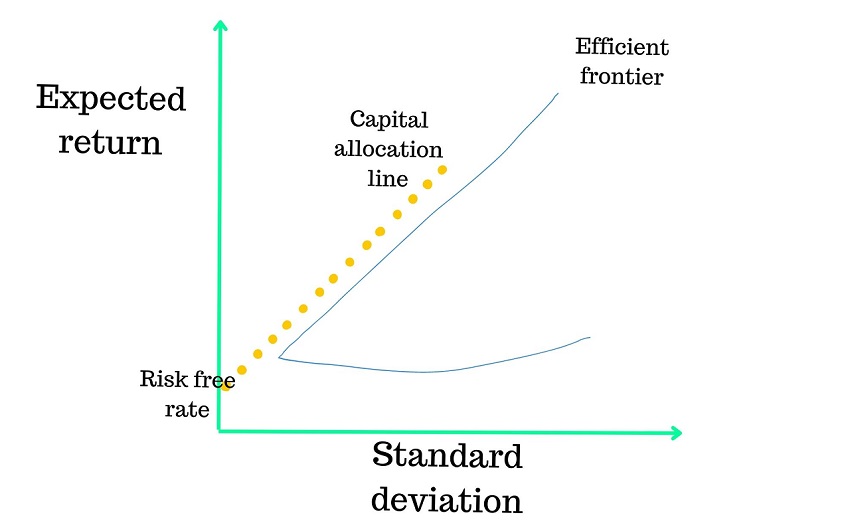
Each point on the frontier, or the deformed C-shaped curve, represents an expected return for a particular level of risk.
Efficient frontier
For an investor, it is the upper portion of the portfolio frontier that matters. This portion is called the efficient frontier and is a combination of points that represents the best possible portfolio of assets for any given level or risk.
Therefore, any portfolio on the efficient frontier offers the highest expected returns for a particular risk level.
Capital allocation line
The capital allocation line is a straight line that measures the risk-reward trade-off for investors. The slope of this line gives provides the increase in expected return per additional unit of standard deviation. Or, in other words, the reward-to-risk ratio.
The slope of this line is called the Sharpe ratio.
As such, Modern Portfolio Theory formula dictates that the point on the efficient frontier which has the highest slope is the optimal portfolio. And the line which joins this point with a point on the Y-axis – the combination of assets which provides a risk-free rate of return – is the best possible capital allocation line.
Advantages of Modern Portfolio Theory
First and foremost, Modern Portfolio Theory helps in the creation of a portfolio without being completely ignorant of the risks. Risk can be difficult to quantify. But by looking at the standard deviation, investors can assign precise numbers to abstract concepts and maximise their gains while keeping the risk at acceptable levels.
Modern Portfolio Theory has also helped grow new-age instruments such as exchange-traded funds. ETFs make it convenient for investors to access a wide range of asset classes. So, a stock investor can reduce the variance of their portfolio by allocating some funds to government bond ETFs as they are negatively correlated with stocks.
Challenges of Modern Portfolio Theory
On the downside, given the amount of maths and statistics needed to calculate key numbers such as variance and slope, the average person can’t really hope to use Modern Portfolio Theory examples to inform their everyday investment decisions. Luckily, one does not need to manually calculate these numbers anymore given the advent of technology since Markowitz wrote his paper way back in 1952.
Critics of Modern Portfolio Theory meaning also question it as an investment tool given its simplistic nature. The variables used by the theory – risk, return, correlation between assets – are based on expected values computed by mathematical models based on historical data. But these models can’t take into account factors that the historical data may not have encountered previously, such as a once-in-a-century pandemic.
Another criticism of Modern Portfolio Theory is that it does not examine portfolios on the basis of the downside risk they may possess. For instance, two portfolios may have the same variance and returns. As such, they will be viewed as equals. However, the variance of one the two portfolios could be explained by frequent small losses, while that of the other could be due to rare but huge losses. Investors may prefer the portfolio with frequent small losses, but the Modern Portfolio Theory views the two portfolios as same.
What is Post-Modern Portfolio Theory?
To account for what some view as flaws in Modern Portfolio Theory, the Post-Modern Portfolio Theory was developed in the early nineties by Brian Rom and Kathleen Ferguson to account for the downside risk mentioned above.
The basis for Post-Modern Portfolio Theory is that portfolio variance may not be the correct way to measure investment risk. Further, it may not be correct for Modern Portfolio Theory to assume that investment returns of all portfolios and assets can be accurately illustrated by what is called a joint elliptical distribution.
- Flat ₹20 Brokerage
- Next-gen Trading
- Advanced Charting
- Actionable Ideas
Trending on 5paisa
Indian Stock Market Related Articles
Disclaimer: Investment in securities market are subject to market risks, read all the related documents carefully before investing. For detailed disclaimer please Click here.

 5paisa Capital Ltd
5paisa Capital Ltd
 5paisa Capital Ltd
5paisa Capital Ltd



