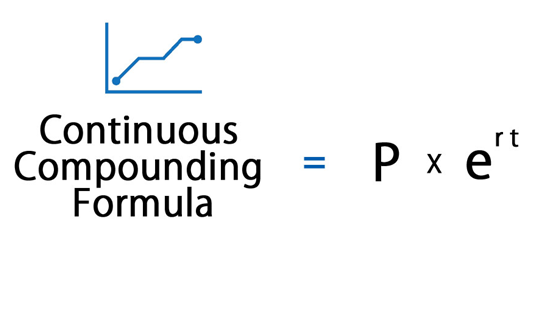Content
- Introduction
- What is Continuous Compounding?
- Importance of Continuous Compounding
- Continuous Compounding Formula
- Calculation of Compounding Formula
- How To Derive Continuous Compounding Formula?
- Conclusion
Introduction
Continuous compounding is needed to calculate the rates of interest, which are crucial to running an economy. People look for the interest percentage before opening an FD account or investing in any portfolio, as the rate of interest is calculated using different means. One of the ways of calculating the interest is through continuous compounding. In this article, let’s understand what is continuous compounding and how you can calculate it.
More Articles to Explore
- Difference between NSDL and CDSL
- Lowest brokerage charges in India for online trading
- How to find your demat account number using PAN card
- What are bonus shares and how do they work?
- How to transfer shares from one demat account to another?
- What is BO ID?
- Open demat account without a PAN card - a complete guide
- What are DP charges?
- What is DP ID in a demat account
- How to transfer money from demat account to bank account
Disclaimer: Investment in securities market are subject to market risks, read all the related documents carefully before investing. For detailed disclaimer please Click here.