Content
In options trading, the “Greeks” play a critical role in helping traders understand and manage risk. Among these Greeks, Gamma is one of the most powerful — yet often misunderstood. It tells you how fast Delta in options will change when the underlying asset moves. For anyone using options in their portfolio, grasping the concept of Gamma is essential, especially if you're relying on Delta trading strategies or managing a Delta neutral strategy.
Unlock the full article - sign in with Gmail!
Expand Your Market Knowledge with 5paisa Articles
What is Gamma in Options Trading?
Gamma measures the rate of change of Delta with respect to the underlying asset’s price. Since Delta tells you how much an option's price will change with a ₹1 move in the underlying stock, Gamma tells you how much Delta itself will change if the stock moves ₹1.
Think of Delta as speed, and Gamma as acceleration. If a car speeds up from 20 km/h to 40 km/h, Gamma is the change in speed — it’s the acceleration (or deceleration) of Delta.
In short:
Delta = how much the option price moves
Gamma = how much Delta moves
How Does Gamma Work?
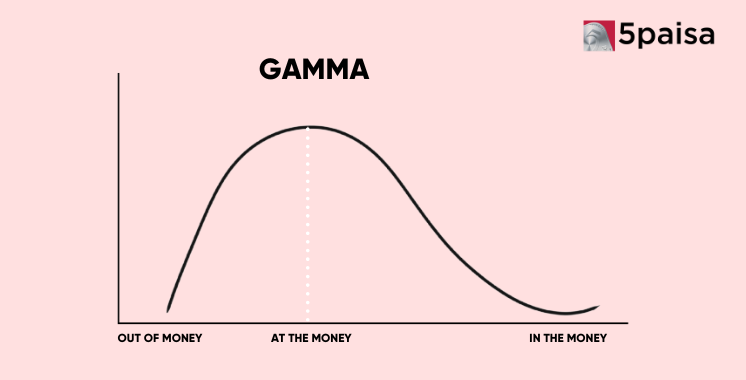
Gamma is always highest for at-the-money (ATM) options and drops as options go deeper in- or out-of-the-money. That’s because small price changes in the underlying asset significantly impact the probability of ATM options finishing in the money. This makes their
Delta sensitive and more likely to shift quickly — hence, high Gamma.
Gamma is more relevant to short-term options because they experience rapid changes in Delta as expiration nears. As time passes and options approach expiry, Gamma becomes more “aggressive” and jumps with even minor movements in the underlying.
Gamma Example: How Option Delta Changes with Price Movement
Let’s say you buy a call option on a stock that’s trading at ₹100.
- Your option has a Delta of 0.50, meaning if the stock goes up ₹1, your option’s price will increase by ₹0.50.
- It also has a Gamma of 0.10. This tells you that every time the stock moves ₹1, your Delta will change by 0.10.
Now here’s how that plays out:
- If the stock moves from ₹100 to ₹101, your Delta will increase from 0.50 to 0.60.
- That means your option is now more sensitive to the stock’s movement — if it moves up another ₹1, the option will now go up by ₹0.60, not ₹0.50.
This is what Gamma does:
It shows you how much the Delta in options is expected to change when the stock price changes.
Think of Delta as how fast your option moves. Gamma tells you how fast the speed is changing.
A good way to imagine this is like a car:
- Delta is your current speed.
- Gamma is how hard you’re pressing the accelerator (or brake).
The harder you press, the faster your speed (Delta) changes.
So if you're driving (trading) in a fast-moving market (volatile conditions), Gamma tells you how quickly your option’s sensitivity (Delta) will react. That’s why traders watch Gamma closely — especially when managing Delta trading strategies or balancing a Delta neutral strategy.
Gamma in Different Options (ATM, ITM, OTM)
Gamma behaves differently depending on where the option is relative to the stock price:
- At-the-money (ATM) options have the highest Gamma. That’s because a small move in the underlying can push the option from out-of-the-money to in-the-money (or vice versa), drastically changing Delta.
- In-the-money (ITM) options have lower Gamma, because Delta is already high (approaching 1 for calls and -1 for puts), so it won’t change much with price movement.
- Out-of-the-money (OTM) options also have low Gamma, because Delta is small (near 0), and a price move won’t affect it much unless the underlying gets very close to the strike price.
Example:
Assume you’re trading a stock at ₹100. You have three call options:
| Option Strike |
Moneyness |
Delta |
Gamma |
| ₹90 |
ITM |
0.85 |
0.05 |
| ₹100 |
ATM |
0.50 |
0.12 |
| ₹110 |
OTM |
0.20 |
0.04 |
In this case:
- The ₹100 ATM option has the highest Gamma.
- The ₹90 ITM option has a high Delta, but a low Gamma — it won’t change much.
- The ₹110 OTM option has low Delta and low Gamma — it’s unlikely to swing unless the price nears ₹110.
Understanding this relationship is crucial when using any Delta option Greek in risk planning or execution.
Gamma Risk: Why It Matters Near Expiry
As options approach expiry, Gamma becomes more volatile. A small price movement can drastically shift Delta, especially for ATM options. This sudden change can amplify profits — or losses — depending on your position.
This phenomenon is often referred to as "Gamma risk", and it’s particularly important for traders holding short options near expiry. If you're short Gamma, a rapid move in the underlying can leave you scrambling to adjust your position, potentially incurring losses.
How to Use Gamma to Your Advantage
Gamma can help traders manage Delta neutral strategies — where the goal is to offset gains or losses in the underlying stock with those in the option. If you’re long Gamma, your Delta position changes in your favor as the underlying moves, allowing you to rebalance and potentially lock in profits.
For example, in Gamma scalping, a trader maintains a neutral Delta and buys or sells the underlying as Delta changes, harvesting small profits from the shifts.
Long Gamma positions (like buying options) benefit from volatility. Short Gamma (like selling options) benefits from stability. So, align your Gamma exposure based on expected market movement.
Wrapping Up: How Gamma Helps You Stay Ahead in Options Trading
Gamma might seem like a secondary option Greek compared to Delta, but it plays a vital role in how your option behaves as the market moves. Whether you're building a Delta trading strategy, selling options for premium, or managing a Delta neutral strategy, understanding Gamma helps you stay a step ahead.
The more you understand how Gamma and Delta interact, the better you’ll be at adjusting your trades — and protecting your capital — when markets shift.